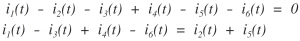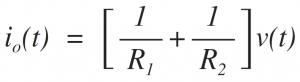An active two-terminal element that supplies energy to a circuit is a source of energy. An ideal voltage source is a circuit element that maintains a prescribed voltage across the terminals regardless of the current flowing in those terminals. Similarly, an ideal current source is a circuit element that maintains a prescribed current through its terminals regardless of the voltage across those terminals.These circuit elements do not exist as practical devices, they are only idealized models of actual voltage and current sources.
Ideal voltage and current sources can be further described as either independent sources or dependent sources. An independent source establishes a voltage or current in a circuit without relying on voltages or currents elsewhere in the circuit. The value of the voltage or current supplied is specified by the value of the independent source alone.In contrast, a dependent source establishes a voltage or current whose value depends on the value of the voltage or current elsewhere in the circuit. We cannot specify the value of a dependent source, unless you know the value of the voltage or current on which it depends.
Figure: (a) An ideal independent voltage source, (b) An ideal independent current source, (c) voltage controlled voltage source, (d) current controlled voltage source, (e) voltage controlled current source, (f) current controlled current source.
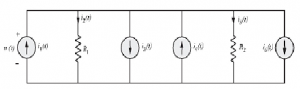
Multiple current source networks
Let us now learn how to reduce a network having multiple current sources and a number of resistors in parallel. Consider the circuit shown in Fig. We have assumed that the upper node is volts positive with respect to the lower node.
Applying KCL to upper node yields,
As a consequence of equation , the network of above Figure is effectively reduced to that shown in Figure below,
Here, the algebraic sum of all current sources present in the multiple source network is given by,
Further, using Ohm's law, the currents on the right side of equation's can be expressed in terms of the voltage and individual resistance so that KCL equation reduces to,
Thus, we can reduce a multiple current source network into a network having only one current source.
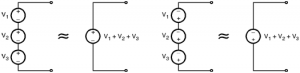
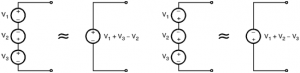
Voltage sources in series :
- When two or more voltage sources are connected in series then the polarity of the resultant voltage source depends on the polarities of the individual source.
- Various possibilities of series connection of voltage sources have been illustrated in below figures,
Current sources in parallel :
If the current sources are in parallel then the magnitude and direction of resultant current source depends on the magnitude and directions of the individual sources. From Figure it is clear that the magnitudes of sources add together if the directions are same and the direction of resultant current source is same as that of the individual sources (see Figs. (a) and (d)). If the directions of individual current sources are opposite to each other, then the resultant current source will have a magnitude (I1 – I2) and the direction will be that of the larger current source of the two.