Home > Analog CMOS Design > MOSFET Fundamentals > Linear Region of Operation

Linear Region of Operation :

Consider a n-channel MOSFET whose terminals are connected as shown in Figure below assuming that the inversion channel is formed (i.e. V _GS > V_TH) and small bias is applied at drain terminal.

Now suppose the drain voltage is greater than zero. As the channel potential varies from '0' at the source to the V_D at the drain, current I_DS starts flowing from the drain to source because of this potential difference.

The local voltage difference between gate and channel now varies from V _G to V_G - V_D. Thus the charge density at point 'x' along the channel can be written as

Q_i (x) = - C_ox [V_GS - V (x) - V _TH]

Where V (x) is the channel potential at 'x' and

C_ox = is the oxide capacitance

with Î_ox = 3.9 ´ Î_o = 3.5 ´ 10^{- 11} F/m and t_ox is the oxide thickness.

I_DS = - n_n (x) × Q_i (x) W

The electron drift velocity is related to the electric field through a parameter called mobility (m_n) as :

n_n = - m_n E (x)

But the electric field E (x) can be expressed as :

E (x) = -

\ n_n (x) = m_n

Substituting Equations (8.3.10) and (8.3.6) in Equation (8.3.7) we get,

I_DS = W C_ox m_n [V_GS - V (x) - V _TH] ×

i.e. I_DS × dx = m_n C_ox W [V_GS - V (x) - V_TH] dV (x)

By using the Boundary conditions,

i.e. V (O) = 0 and V (L) = V_DS

and integrating the Equation over the length of channel 'L' we get,

I_DS × dx = m_n C_ox W [V_GS - V (x) - V _TH] × dV (x)

Assuming mobility (m_n) and threshold voltage (V_TH) constant over 'x' we get,

I_DS = m_n C_ox

Here the product of m_n and C_ox is called as the process transconductance parameter given as :

K_n¢ = m_n C_ox =

The product of process transconductance (K_n¢) and the ratio of an transistor is called as the gain factor (K_n) given as :

K_n = K_n¢ × = m_n C_ox

Therefore the drain to source current equation becomes :

I_DS = m_n C_ox = K_n¢

= K_n

The operating region where Equation holds is called as resistive or linear region of operation.

The important point here to note that 'L' is the effective channel length.

The I_D - V_DS relation given by Equation represents a parabola which is plotted as shown in Figure below shows for various values of V_GS and indicates that the current capability of device increases with V_GS.

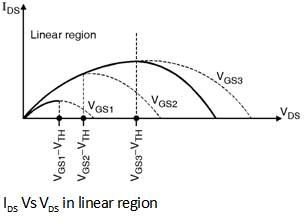
By calculating and equating to zero, we get that the peak of each parabola occurs at V_DS = V_GS - V_TH and the peak current is,

I_DSmax = m_n C_ox (V_GS - V _TH)²

The difference (V_GS - V_TH) is called as the “overdrive voltage” and the ratio is called as the “aspect ratio”. If V _DS £ (V_GS - V_TH) then the device is said to be operate in triode region.

If in Equation , V_DS << 2 (V_GS - V_TH ),

We have, I_DS » m_n C_ox (V_GS - V _TH) V_DS

i.e. The drain to source current is a linear function of V_DS for small values of V_DS and each parabola from above Figure can be approximated by a straight line. The linear relationship implies that the path from the source to the drain can be represented by a linear resistor given as :

R_on =

Thus a MOSFET can be operated as a resistor whose value is controlled by overdrive voltage (V_GS - V_TH).