State Minimization :

State Minimization : Whenever we design any circuit, in initial stage we say it as “Raw” design. Once the “Raw” design fulfills our requirements, we concentrate on reducing the same design. Reducing doesn't mean compromising for performance. Reducing means reduction in hardware. By reducing hardware one can reduce cost of the equipment and increase reliability of the design. Reliability increases with less components because failure rate decreases. In sequential system design we would also like to reduce the hardware. But for reducing the same we have to use procedure or algorithm, this process is called “State table reduction.” The name involve state table just because we are going to take help of state table and reduce the number of states. To understand the concept more clearly let's take one example. 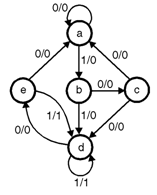Example 1: For given state diagram, prepare state table and reduce the same using “State table reduction” technique.

(1) The first step we will follow is to prepare state table. The state table is as follows : Present state Next state Output x = 0 x = 1 x = 0 x = 1 a a b 0 0 b c d 0 0 c a d 0 0 d e f 0 1 e a f 0 1 f g f 0 1 g a f 0 1 Now observe the state table carefully. Can you see “equivalent state(s)” ? Yes, states g and e are equivalent states; they both go to states a and f, and have outputs of 0 and 1, for x = 0 and x = 1. Change in the state table is “discard” state g and replace state g by e therefore we have new table as, Present state Next state Output x = 0 x = 1 x = 0 x = 1 a a b 0 0 b c d 0 0 c a d 0 0 d e f 0 1 e a f 0 1 f e f 0 1 'g' state replaced by 'e' Now again observe this new table carefully. Can you find any “equivalent state” ? Yes, 'd' and 'f' both are same. Therefore now discard state f, and replace state f in state diagram by state 'd'. Therefore next version of state table is as follows : Present state Next state Output x = 0 x = 1 x = 0 x = 1 a a b 0 0 b c d 0 0 c a d 0 0 d e d 0 1 e a d 0 1 Now prepare state diagram for reduced state table.