Dynamic Hazards

• The other type of hazard associated with the combinational networks is called as a dynamic hazard.
• It also has the same effect as that of static hazards i.e. false output.
• Dynamic hazards occur when the output of the circuit is to change from one logic level to the other one but a momentary false output signal occurs during the transient behaviour.
• The dynamic hazards are illustrated in Figure below.

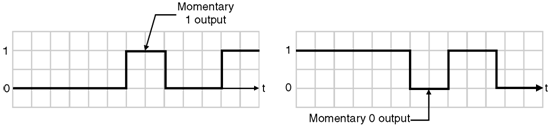
Definition of Dynamic Hazard :

We can define the dynamic hazard as a transient change which occurs three or more times at the output of a logic circuit, when the output is supposed to change only once during the transition between two inputs states which differ in the value of one variable. Illustration of Dynamic Hazards :

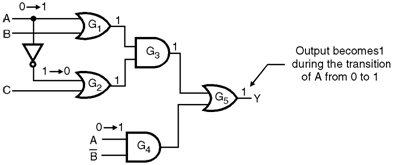
• Consider the network shown in Figure below. It can be proved that this network is free from static 0 as well as static 1 hazards.
  
  Steady state behaviour :
• Consider the input states ABC = 000 and ABC = 100. For ABC = 000, the steady state output is, Y = [ (A + B)  (A– + C) ] + (A  B– ) = [ (0 + 0)  (1 + 0)] + (0  1) = [0  1] + (0) = 0
• For ABC = 100, the steady state output is, Y = [(1 + 0)  (0 + 0)] + (1  1) = [ (1  0) ] + (1)  Y = 1

  Transient behaviour :

• For understanding the transient behaviour, assume that the gates G3 and G5 do not have any propagation delays.
• The propagation delays of the other gates are as follows : (1) G1 switches faster than G2. (2) G2 can switch faster than G4.
• That means G1, G2 and G4 have finite propagation delays. The delay of G4 is longest and that of G1 is shortest. When A changes from 0 to 1 :
• When A changes from 0 to 1 the events taking place are as follows : 1. This change propagates through G1 before G2. 2. The input to G3 are simultaneously 1. 3. The output Y changes from 0 to 1.
• This is shown in Figure below.
• Then when change in A propagates through gate G2, the lower input to G3 becomes zero and the network output again returns back to 0.
• Finally when A = 1, the signal propagates through gate G4 to make the lower input to the gate G5 equal to 1 and the Y output again becomes 1.
• Thus during the transition of input variable A, the output Y changes 0 ï‚® 1 ï‚® 0 ï‚® 1 and the dynamic hazard is said to have occured.
• The detection of dynamic hazards is more difficult than that of the static hazards.
• They produce false outputs. Their severity depends on the devices or systems receiving them.
  
  
• The false outputs in the combinational logic of asynchronous sequential networks can cause malfunctions.
• So combinational logic circuits which are specially designed for static hazard free operation can also be free of dynamic hazards.