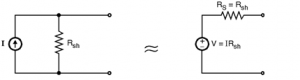Source transformation is a procedure which transforms one source into another while retaining the terminal characteristics of the original source. Source transformation is based on the concept of equivalence. An equivalent circuit is one whose terminal characteristics remain identical to those of the original circuit. The term equivalence as applied to circuits means an identical effect at the terminals, but not within the equivalent circuits themselves.
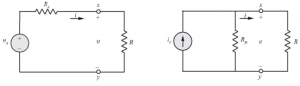
In above figure we require both the circuits to have the equivalence or same characteristics between the terminals x and y for all values of external resistance R. We will try for equivalence of the two circuits between terminals x and y for two limiting values of R namely R = 0 and R = ∞. When R = 0, we have a short circuit across the terminals x and y . It is obligatory for the short circuit to be same for each circuit. The short circuit current of the figure is
is=vs/Rs
Applying KVL to Fig.
Source Shift
The source transformation is possible only in the case of practical sources. i.e and
, where Rs and Rp are internal resistances of voltage and current sources respectively. Transformation is not possible for ideal sources and source shifting methods are used for such cases.
Voltage source shift (E-shift):
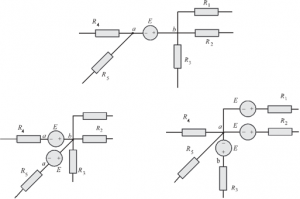
Consider a part of the network shown in Figure that contains an ideal voltage source.
Since node is at a potential E with respect to node a, the network can be redrawn equivalently as in the figures depend on the requirements.
Current source shift (I shift)
In a similar manner, current sources also can be shifted. This can be explained with an example. Consider the network shown in Figure, which contains an ideal current source between nodes a and c. The circuits shown in Figure illustrates the equivalent circuit after the I – shift.
Transformation of independent voltage source to independent current source :
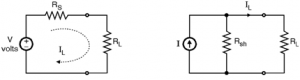
The practical voltage source shown in Figure is to be transformed into an equivalent current source.
Steps to be followed :
Step 1 : Calculate the load current IL for the voltage source.
Step 2 : Obtain expression for load current IL for the current source.
Step 3 : Equate the two load currents and obtain expressions for I and Rsh and draw the equivalent source.
Transformation of current source to voltage source :
We will follow the same steps followed for the transformation of a voltage source to current source and we get,
V = IRsh and RS = Rsh
Thus the magnitude of the voltage of equivalent voltage source will be IRsh and the internal series resistance is RS = Rsh. The equivalent voltage source is as shown in Figure.
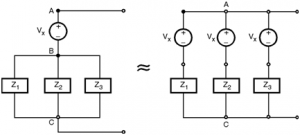
Voltage source shifting :
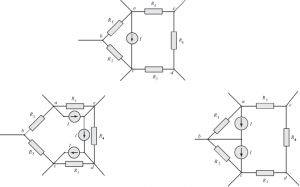
Consider the partial network shown in Figure. Note that there is no series impedance present in the branch AB in which the source Vx is connected. Hence we can't convert Vx into an equivalent current source.
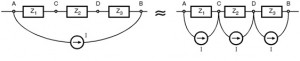
Current source shifting :
Consider the partial network of Figure. Note that there is no direct parallel impedance present in the branch AB in which the current source I is connected. Hence it is not possible to convert current source I into an equivalent voltage source.
The current source I is connected across each impedance as shown in Figure.