Home > combinational logic circuits > full subtractor

Full Subtractor

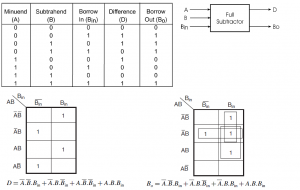
Full subtractor performs subtraction of two bits, one is minuend and other is subtrahend. In full subtractor '1' is borrowed by the previous adjacent lower minuend bit. Hence there are three bits are considered at the input of a full subtractor. There are two outputs, that are DIFFERENCE output D and BORROW output Bo. The BORROW output indicates`that the minuend bit requires borrow '1' from the next minuend bit. Figure shows the truth table of a full
subtractor. The K-maps for the two outputs are shown in figure. If we compare DIFFERENCE output D and BORROW output Bo with full adder`it can be seen that the DIFFERENCE output D is the same as that for the SUM output. Further, the BORROW output Bo is similar to CARRY-OUT. In the case of a half-subtractor, A input is complemented similar things are carried out in full subtractor. Fugure below shows the block diagram of the full subtractor. The inputs of the full subtractor are A, B and Bin . The outputs of the full subtractor are D and Bo.

Figure below shows the truthtable of the full subtractor.

1) When the inputs minuend (A) =0, Subtrahend (B) =0 and Borrow in (Bin) = 0 then the difference (D) = 0 and Borrow out (Bo) =0

2) When the inputs minuend (A) =0, Subtrahend (B) =0 and Borrow in (Bin) = 1 then the difference (D) = 1 and Borrow out (Bo) =1

3) When the inputs minuend (A) =0, Subtrahend (B) =1 and Borrow in (Bin) = 0 then the difference (D) = 1 and Borrow out (Bo) =1

4) When the inputs minuend (A) =0, Subtrahend (B) =1 and Borrow in (Bin) = 1 then the difference (D) = 0 and Borrow out (Bo) =1

5) When the inputs minuend (A) =1, Subtrahend (B) =0 and Borrow in (Bin) = 0 then the difference (D) = 1 and Borrow out (Bo) =0

6) When the inputs minuend (A) =1, Subtrahend (B) =0 and Borrow in (Bin) = 1 then the difference (D) = 0 and Borrow out (Bo) =0

7) When the inputs minuend (A) =1, Subtrahend (B) =1 and Borrow in (Bin) = 0 then the difference (D) = 0 and Borrow out (Bo) =0

8) When the inputs minuend (A) =1, Subtrahend (B) =1 and Borrow in (Bin) = 1 then the difference (D) = 1 and Borrow out (Bo) =1

The Karnaugh maps for the for DIFFERENCE output D is shown in figure as it is clear from the Karnaugh maps, no simplification is possible for the difference output D. The expression for difference (D) is also shown in figure.

The Karnaugh maps for BORROW output Bo is shown in figure below. As it is clear from the two Karnaugh maps, simplification is possible for the BORROW output Bo. The simplified expression for Bo is also shown in figure.

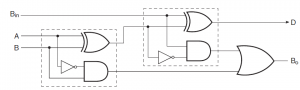
Figure below shows the logic level implementation of full subtractor using logic gates.

When we compare the expressions of the full subtractor and the full adder we can see that, the

expression for DIFFERENCE output D is the same as that for the SUM output of the full adder. Further, the expression for BORROW output Bo of the full subtractor is same as that of the expression for CARRY-OUT Co of the full adder. In half-subtractor, the A input is complemented. Therefore we can see that, the full subtractor can also be implemented by using the two half-subtractors. The implementation of full subtractor using the two half subtractors is shown in figure below. In this implementation two half subtractors and on OR gate used.

The four bit subtracor can be implemented by using the full subtractor. Figure below shws the implementation of four bit binary subtractor. Here, the A0, A1,A2, A3 are the minuend and the B0,B1,B2,B3 are the subtrahend. Bin is the Borrow in. The output of the four bit binary subtractor is difference D0, D1, D2 D3. The Bout is the borrow out.

points to remember

Figure below shows the implementation of full subtractor using logic gates.