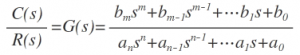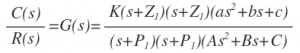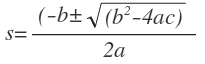Transfer Function:
Mathematically Transfer Function is defined as the ratio of Laplace transform of output of the system to the Laplace transform of input under the assumption that all initial conditions are zero.
Symbolically system can be given as below and its transfer function of system can be shown as given below,
G(s) = Laplace transform of output/ Laplace transform of input
= C(s) / R(s) = L[ c(t)] / L[r(t)]
By taking Laplace transform of the differential equations for nth order system,
Characteristic Equation of a transfer function:
Characteristic Equation of a linear system is obtained by equating the denominator polynomial of the transfer function to zero. Thus the Characteristic Equation is,
Poles and zeros of transfer function :
From the equation above the if denominator and numerator are factored in m and n terms respectively the equation is given as,
Poles:
The poles of G(s) are those values of ‘s’ which make G(s) tend to infinity e.g. in the equation above there are poles at s= -p1 , s= -p2 and a pair of poles at
Zeros:
The zeros of G(s) are those values of ‘s’ which make G(s) tend to zero e.g. in the equation above there are zeros at s= -Z1 , s= -Z2 and a pair of zeros at,
If either poles or zeros coincide, then such poles and zeros are called multiple poles or zeros else they are called simple poles .
If the number of zeros are less than the number of poles i.e. Z < P then the value of transfer function becomes zero for s—> ∞ hence we can say that there are zeros at infinity and the number of such zeros is (P-Z )
If the number of poles are less than the number of zeros i.e. Z > P then the value of transfer function becomes infinity for s—> ∞ hence we can say that there are poles at infinity and the number of such poles is (Z-P )