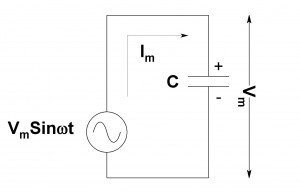
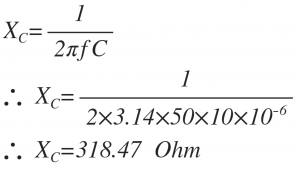In the AC analysis of capacitors we have seen that, the current flowing through the capacitor is directly propotional to the rate of change of the supply voltage. Hence in the supply voltage if sine wave is used then the current waveform will be the cosine wave. However, although the current is flowing through the circuit, this current is opposed by the some resistance. This kind of opposition to the flow of current is called as the capacitive reactance. Therefore, in AC circuits shown below the capacitor also has the capacitive reactance.
Capacitive Reactance is only available in capacitor based AC circuits and restricts to the flow of alternating current. Similar to resistive resistances the capacitive reactancs are also measured in Ohm. The reactance is normally denoted by the symbol X. However, since the reactance term is also used for inductors the capacitive reactance is denoted by “Xc”. As we have seen in the AC circuits the capacitance of the capacitor depends upon the positive and negative half cycles of the supply voltage, the capacitive reactance is depends upon the frequency of operation of the supply voltage. The capacitive reactance is given by,
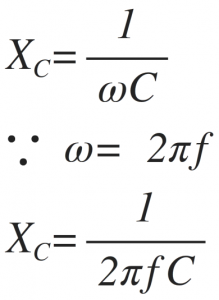
Here,
ω is the angular frequency in Radian,
f is the operating frequency of AC supply voltage in Hertz,
C is the capacitance in Farads.
From the above equation it can be seen that, the capacitive reactance is inversely proportional to the supply frequency and the capacitance value of the capacitor. As the capacitor value increases the capacitive reactance decreases. Also, as the supply frequency increases the capacitive reactance decreases. Hence, for frequency reaches to infinity the capacitive reactance reduces to zero and acts as a short circuit i.e zero resistance. When frequency reaches to zero the capacitive reactance increases to infinity and acts as a open circuit i.e. infinite resistance. The variation of capacitive reactance as a function of frequency is shown in figure below,
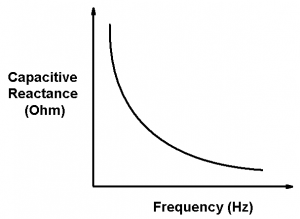
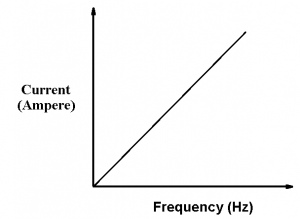
The above figure shows that, capacitive reactance of the capacitor decreases as the supply frequency of the voltage supply used in the AC circuit increases. This clearly shows that, capacitive reactance is inversely proportional to the supply frequency of the applied AC signal. Also when the supply frequency of the voltage supply used in the AC circuit increases the current flowing in the circuit increases linearly. This increase in the current flowing through the AC circuit is mainly because of the voltage change across the two metallic plates of the capacitor. Figure bellow shows the variation of current with respect to the supply frequency of the AC circuit.
Solved Problems:
1) Calculate capacitive reactance in the AC circuit if C= 10 µF and supply voltage is 230V, 50 Hz.
As we know that,