In order to produce complex circuits the equivalent inductance can be found out using the combination of individual inductors. The individual inductors can be connected in series combination or parallel combination. In series combination the inductors are connected back to back whereas in the parallel combination the inductor termenials are connected in the parallel form. However, in series or parallel combination of the inductors facts of no mutual inductance or magnetic coupling between the individual inductors is considered. The inductors are connected in series when they are daisy chained in a straight line by connecting end to end. As in the resistors series combination the different resistances connected together in series are added together. Similarly in the series combination of inductors also inductances are added together. This is mainly because the number of coil turns are increased in the series combination of the inductors. Hence, the equivalent inductance of the series combination of the inductors is the addition of the individual inductances of the connected inductors. Figure below shows the series combination of the four inductors,

The current, ( I ) that flowing through the first inductor, L1 way to pass through the second inductor, third inductor and fourth inductor. Hence, in series combination of inductors the same current flows through the inductors.
![]()
Hence in the above series combination of inductors the inductors L1, L2 , L3 and L4 are all connected together in series. Therefore, the sum of the individual voltage drops across each inductor is given by,
As we know from in an inductor the self-induced emf across an inductor is given by,
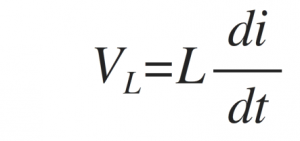
Therefore, by considering the individual voltage drops across each inductor, the total voltage drop for the series combination is given by,
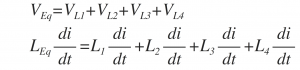
Dividing through out the above equation by di/dt we will get,
![]()
Thus, the equivalent inductance of the series combination of the inductors is the sum of all the individual inductances of the series connected inductors. However, the above equation true only when no mutual inductance or magnetic coupling between two or more of the inductors is available in the inductors. Hence, in series combination of the inductors, the equivalent inductance of the series combination is larger than the individual inductance values of the inductors.
Series combination of Mutually Coupled Inductors
In series combination of inductors when magnetic field of one inductor is linked with the other, the mutual inductance of the combination leads to either increase in equivalent inductor or decrease in the equivalent inductance of the series combination. The equivalent inductance of this series combination depends upon the amount of magnetic coupling between the inductors involved in the series combination. The mutual inductance depends upon the distance between the individual inductor coils and the orientation of the inducting coils used in the series combination of the inductors. The mutually connected series inductors can be classified as either “Aiding†or “Opposing†the total inductance of the series combination. When the magnetic flux produced by the current through the coils in the same direction then that coils are called as cumulatively coupled coils whereas when the current flowing through the coils in opposite directions then the coils are called as differentially coupled coils. Figure below shows the cumulatively coupled coils and differentially coupled coils
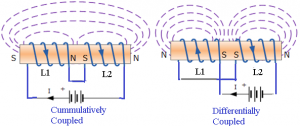
When the inductors are cumulatively coupled then the equivalent inductance is given by,
![]()
When the inductors are differentially coupled then the equivalent inductance is given by,
![]()
Hence the equivalent capacitance in the mutually coupled inductors in series combination is given as,
![]()